How to Implement Binary Heap Data Structure Using Python

Last updated: September 15, 2024 By Sunil Shaw

A binary heap is a binary tree. A complete trees has all levels completely filled except possibly the last level. It also means that the trees balances. Let’s see How to Implement Binary Heap Data Structure Using Python.

Insert every new items next to the available space, and store a Binary heap in an array.

A binary heap can be of two types: Min Heap or Max Heap. In case of Min Heap binary heap, the root node is the minimum of all the nodes in the binary heap, all parent nodes are smaller than their children. On the other hand in case of Max Heap the root is the maximum among all the keys present in the heaps, and all nodes are bigger than their child.

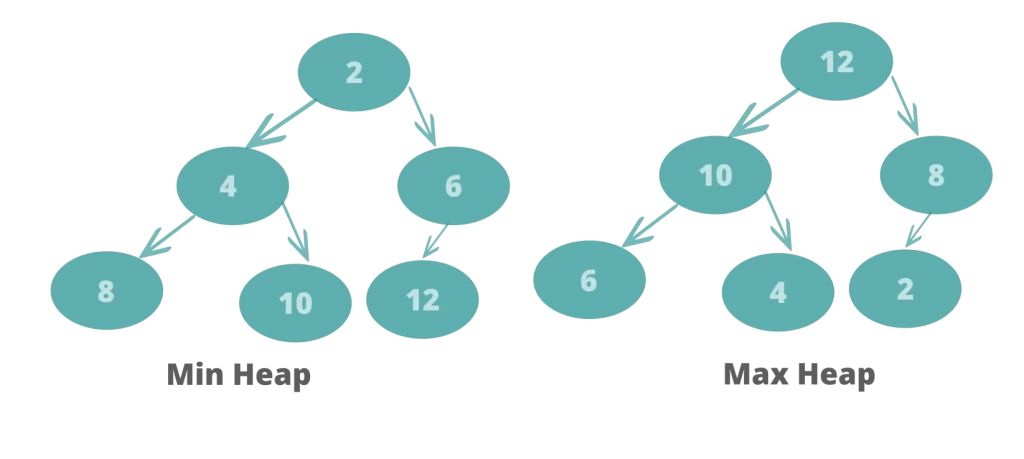
Heap has two important properties:

It is complete and is constructed from left to right across each row and the last row may not be completely full. Each row should be filled up sequentially. So, the order of inserting values should be from left to right, row by row sequentially as shown in the below figures:

How to Implement Binary Heap Data Structure Using Python

2. The parent must be larger in case of Max Heap and smaller in case of Min Heap than the children.

Look at the above figures. it is a case of Maximum heap because all parents are greater than their children.

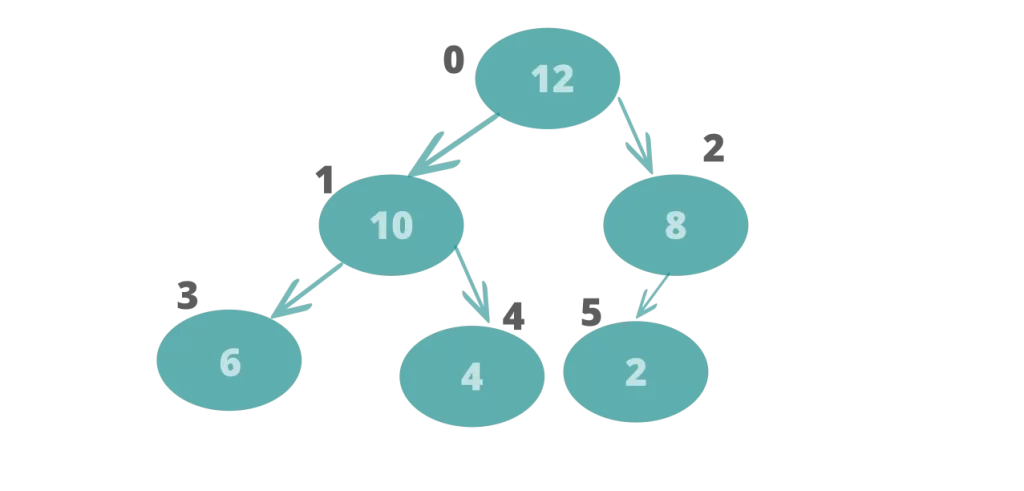
The binary heap can be represented in an array as follows:

If you look at the array carefully you will realize that if a parent exists at location n then the left child is at 2n+1 and right child is at 2n + 2.

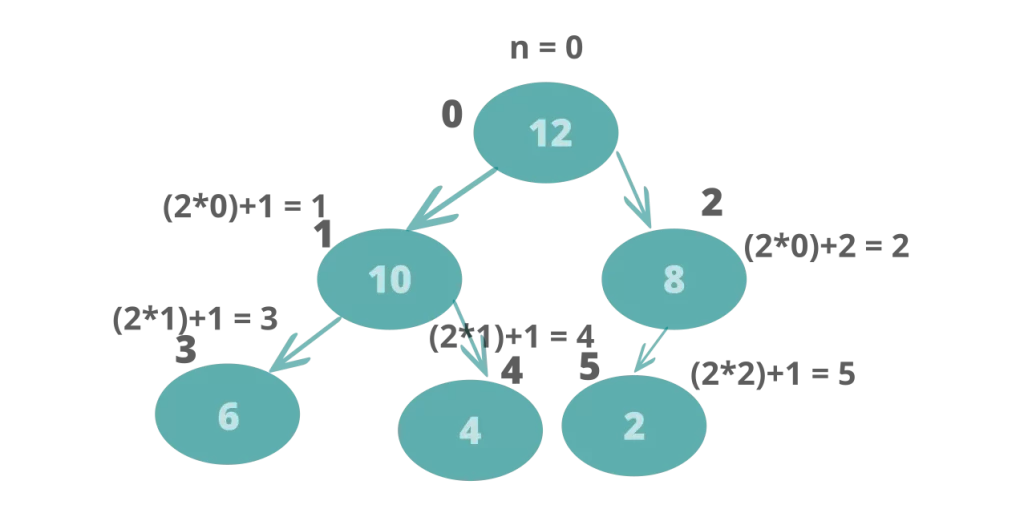
So, if we know the location of the parent child we can easily find out the location of the left and right child.

Now suppose we have to build up a Max HEap using following values:

20, 4, 90, 1, 25

Step 1

Insert 20

Step 2

Insert 4 -> Left to Right -> First element in second row

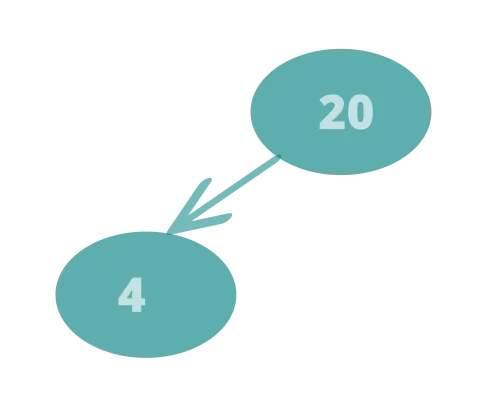
Since the parent is greater than the child, this is fine.

Step 3

Insert 90 -> Left to Right -> Second element in seconf row

However, when we insert 90 as the right child, it violates the rule of the max heap because the parent has a key value of 20. So, in order to resolve this problem it is betterto swap places as shown in the following figures.

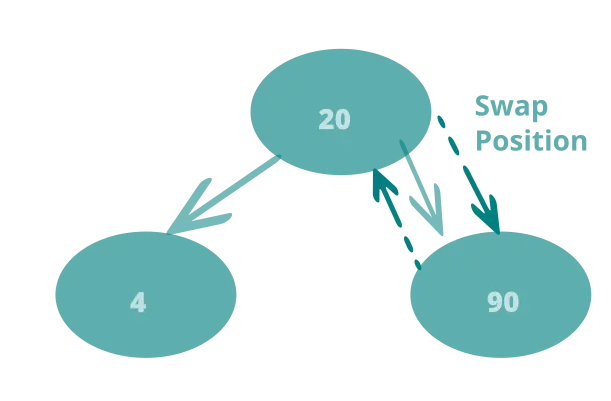
After swapping, the heap would look something like this:

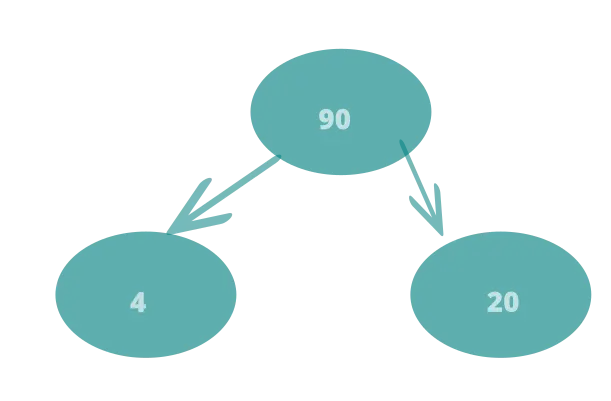
Insert 1 -> left to right -> first element third row

since 1 is smaller than the parent node, this is fine.

Step 5

insert 125

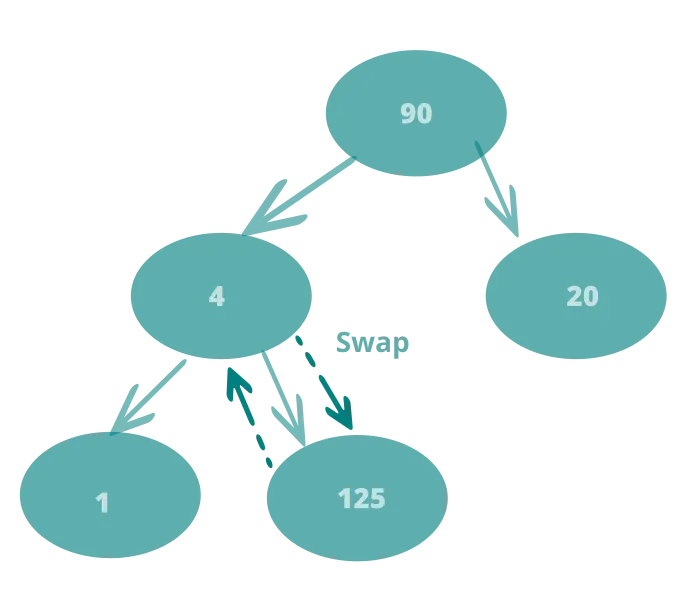
This violated the rule of Max Heap

Swap 4 and 125

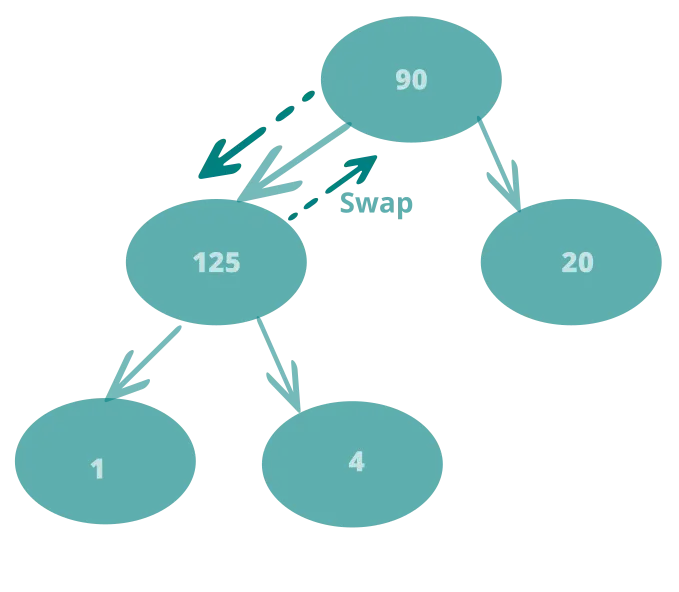
Not a heap still Swap 125 and 90

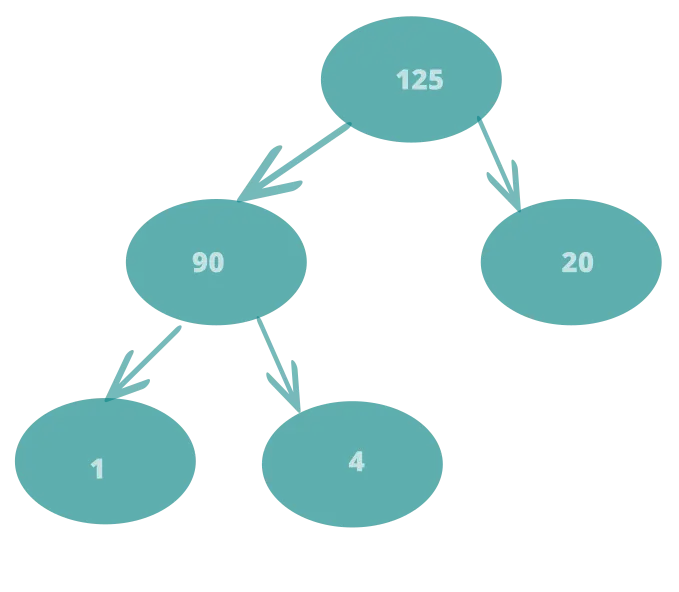
We now have a Max Heap.

Example 12.1

Write python code to implement Max HEap. How would you insert a value so that the root node has the maximum value and all parent are greater than their children.

Here we will write the code ti implement MaxHeap class. The class will have two functions:

Push(): To insert value.

Float_up(): To place the value where is belongs>

Step 1

Define the class

class MaxHeap:

Step 2

Define the Constructor

	def __init__(self):
		self.heap = []

Step 3

Define the push() function.

The push function does two jobs:

Appends the value at the end of the list. (We have seen earlier that the value hav to be inserted first at the available location)
After appending the value, the push() function will call the float_UP(index) function. The push() function passes the index of the last element to the float_up() function so that the float_up() function can analyse the values and do the needful as described in the next step.

	def push(self, value):
		self.heap.append(value)
		self.float_up(len(self.heap)-1)

Step 4

Define the float_up() function

1. The float_up() function takes index value as parameter.

	def float_up(self, index):

2. The push() function passes the index value of the last element in the heap. The first thing that the float_up function does is that it checks if the element is at index 0 or not. If yes, thenit is the root node. Root node has no parents and since it’s the last element of the heap it has no children either. So, we can return the value.

		if index == 0:
			return

3. If the index is greater than 0 then we can proceed further. Look the below figure once again.

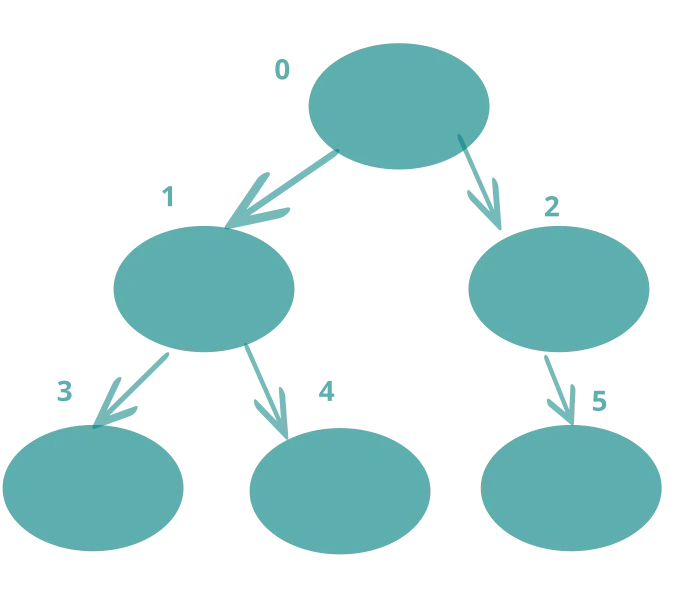
For programming, you need to understand few things.

The index 0 has two children at position 1 and 2. If there is an element at 1 then you can find the parent by calculating value of(1/2). Similarly for element at index 2, the parent’s index value can be found out by calculating value of(2/2-1). So, we can say that if an element has an odd index value then it’s parent’s index value is defined as parent_of_index= index//2. However, if its index value is even then parent_of_index will be equal (index//2)-1. This becomes the outer frame for the float_up function. The right child has an even number as index and the left child has an odd number as index.

			if index%2 == 0:
				parent_of_index = (index//2)-1
				if self.heap[index]> self.heap[parent_of_index]:
					self.swap(index, parent_of_index)
				else:
					parent_of_index = index//2

4. Now, we compare the values of the child and the parent. If the child is greater than the parent, swap the elements.

	def float_up(self, index):
		if index == 0:
			return
		else:
			if index%2 == 0:
				parent_of_index = (index//2)-1
				if self.heap[index]> self.heap[parent_of_index]:
					self.swap(index, parent_of_index)
				else:
					parent_of_index = index//2
					if self.heap[index]> self.heap[parent_of_index]:
						self.swap(index, parent_of_index)
					self.float_up(parent_of_index)

Step 5

Define the swap function.

The swap() function helps in swapping the values of the parent and the child. The code for this is given as follows:

def swap(self, index1, index2):
		temp = self.heap[index1]
		self.heap[index1] = self.heap[index2]
		self.heap[index2] = temp

Code

class MaxHeap:
	def __init__(self):
		self.heap = []

	def push(self, value):
		self.heap.append(value)
		self.float_up(len(self.heap)-1)

	def float_up(self, index):
		if index == 0:
			return
		else:
			if index%2 == 0:
				parent_of_index = (index//2)-1
				if self.heap[index]> self.heap[parent_of_index]:
					self.swap(index, parent_of_index)
				else:
					parent_of_index = index//2
					if self.heap[index]> self.heap[parent_of_index]:
						self.swap(index, parent_of_index)
					self.float_up(parent_of_index)
	def peek(self):
		print(self.heap[0])

	def pop(self):
		if len(self.heap)>= 2:
			temp = self.heap[0]
			self.heap[0] = self.heap[len(self.heap)-1]
			self.heap[len(self.heap)-1]
			self.heap.pop()
			self.down_adj()
		elif len(self.heap) == 1:
			self.heap.pop()
		else:
			print("Nothing to pop")

	def swap(self, index1, index2):
		temp = self.heap[index1]
		self.heap[index1] = self.heap[index2]
		self.heap[index2] = temp

Execution

H = MaxHeap()
print("************* pushing values ****************")
print("pushing 165")
H.push(165)
print(H.heap)
print("pushing 60")
H.push(60)

print(H.heap)

print("pushing 179")
H.push(179)
print(H.heap)

print("pushing 400")
H.push(400)
print(H.heap)

print("pushing 6")
H.push(6)
print(H.heap)

print("pushing 275")
H.push(275)
print(H.heap)

Output

************* pushing values ****************
pushing 165
[165]
pushing 60
[165, 60]
pushing 179
[179, 60, 165]
pushing 400
[179, 60, 165, 400]
pushing 6
[179, 165, 60, 400, 6]
pushing 275
[179, 165, 60, 400, 6, 275]

Example 2.2

Write the code to find out the maximum value in the Max heap.

It is easy to find the max value in the max heap as the maximum value is available at the root node which is index 0 of the heap. If you call the function peek()in previous example it will display the maximum value of the heap.

	def peek(self):
		print(self.heap[0])

Example 2.3

Write the code to pop the maximum value from Max Heap.

There are two steps involved.

Swap the root with the last element in the array and pop the value.
The root node now does have the maximum value. So, now we need to move downwards, comparing the parent with their left and right child to ensure that the children are smaller than the parent. If not we will have to swap places again.

Step 1

Define pop() function

The pop() functionwhich swaps the values of the root node with the last element in the list and pops the value. The function then class the down_adj() function which moves downwards and adjusts the values. The pop() function first check the size of the heap. If the length of the heap is 1 then that means that it only contains one element that’s the root and there is no need to swap further.

	def pop(self):
		if len(self.heap)>= 2:
			temp = self.heap[0]
			self.heap[0] = self.heap[len(self.heap)-1]
			self.heap[len(self.heap)-1]
			self.heap.pop()
			self.down_adj()
		elif len(self.heap) == 1:
			self.heap.pop()
		else:
			print("Nothing to pop")

Step 2

Define down_adj() function

Set index value to 0.

Index of left child = left_child = index*2+1

Index of right child = right_child = index*2+2

Then we go through loop where we check the value of the parent with both left and right child. If the parent is smaller than the left child then we swap the value. We then compare the parent value with the right child, if it is less then we swap again.

This can be done as follows:

Check if parent is less than left child:
- If yes, check if left child is less than the right child
- If yes, the swap the parent with the right child
- Change the value of index to value of right_child for further assessement
If not he just swap the parent with the left child
Set the value of index to value of left_child for further assessement
If the parent is not less than left child but only less than the right child then swap values with the right child.
change the value of index to right_child.

	def down_adj(self):
		index = 0
		for i in range(len(self.heap)//2):
			left_child = index*2+1
			if left_child > len(self.heap)-1:
				print(self.heap)
				print("End Point")
				print("HEap value after pop() = ", self.heap)
				return

			right_child = index*2+2

			if right_child > len(self.heap)-1:
				print("right child does not exist")

				if self.heap[index] < self.heap[left_child]:
					self.swap(index, left_child)
					index = left_child
					print("Heap value fater pop() = ", self.heap)
					return


				if self.heap[index] < self.heap[left_child]:
					if self.heap[left_child] < self.heap[right_child]:
						index = right_child

					else:
						self.swap(index, left_child)
						index = left_child

				elif self.heap[index] < self.heap[right_child]:
					self.swap(index, right_child)
					index = right_child

				else:

					print("No Change required")

			print("Heap value after pop() = ",self.heap)

Code

class MaxHeap:
	def __init__(self):
		self.heap = []

	def push(self, value):
		self.heap.append(value)
		self.float_up(len(self.heap)-1)

	def float_up(self, index):
		if index == 0:
			return
		else:
			if index%2 == 0:
				parent_of_index = (index//2)-1
				if self.heap[index]> self.heap[parent_of_index]:
					self.swap(index, parent_of_index)
				else:
					parent_of_index = index//2
					if self.heap[index]> self.heap[parent_of_index]:
						self.swap(index, parent_of_index)
					self.float_up(parent_of_index)
	def peek(self):
		print(self.heap[0])

	def pop(self):
		if len(self.heap)>= 2:
			temp = self.heap[0]
			self.heap[0] = self.heap[len(self.heap)-1]
			self.heap[len(self.heap)-1]
			self.heap.pop()
			self.down_adj()
		elif len(self.heap) == 1:
			self.heap.pop()
		else:
			print("Nothing to pop")

	def swap(self, index1, index2):
		temp = self.heap[index1]
		self.heap[index1] = self.heap[index2]
		self.heap[index2] = temp

	def down_adj(self):
		index = 0
		for i in range(len(self.heap)//2):
			left_child = index*2+1
			if left_child > len(self.heap)-1:
				print(self.heap)
				print("End Point")
				print("HEap value after pop() = ", self.heap)
				return

			right_child = index*2+2

			if right_child > len(self.heap)-1:
				print("right child does not exist")

				if self.heap[index] < self.heap[left_child]:
					self.swap(index, left_child)
					index = left_child
					print("Heap value fater pop() = ", self.heap)
					return


				if self.heap[index] < self.heap[left_child]:
					if self.heap[left_child] < self.heap[right_child]:
						index = right_child

					else:
						self.swap(index, left_child)
						index = left_child

				elif self.heap[index] < self.heap[right_child]:
					self.swap(index, right_child)
					index = right_child

				else:

					print("No Change required")

			print("Heap value after pop() = ",self.heap)

Execution

************* pushing values ****************
pushing 165
[165]
pushing 60
[165, 60]
pushing 179
[179, 60, 165]
pushing 400
[179, 60, 165, 400]
pushing 6
[179, 165, 60, 400, 6]
pushing 275
[179, 165, 60, 400, 6, 275]
********************** popping value *************************
Heap value after pop() =  [275, 165, 60, 400, 6]
Heap value after pop() =  [275, 165, 60, 400, 6]
Heap value after pop() =  [6, 165, 60, 400]
Heap value after pop() =  [6, 165, 60, 400]
Heap value after pop() =  [400, 165, 60]
right child does not exist
Heap value after pop() =  [165, 60]
Nothing to pop

Example 12.4

What are the appliactions of binary heap ?

Dijkstra algorithm
Prims algorithm
Priority queue
Can be used to solve problems such as:
- K’th largest element in an array
- Sort an almost sorted array
- Merge K sorted array

Example 12.5

What is a priority queue and how can it be implemented?

Priority queue is like a queue but it is more advanced. It has methods same as a queue. However, the main difference is that it keeps the value of higher priority at front, and the value of lowest priority at the back. Add items from the rear and remove them from the front. In a priority queue, add element in order. So, basically there is a priority associated with every element. Element of highest priority is removed first. Elements of equal priority are treated as per their order in queue.

Conclusion

In this articles you learnt How to Implement Binary Heap Data Structure Using Python. Trees on the other hand are hierarchial data structures. Searching information on trees is faster than linked lsits.

How to implement Tree Data Structure Using Python