How to implement Tree Data Structure Using Python

Last updated: September 13, 2024 By Sunil Shaw

Introduction

You can use several types of data structure to tackle applications problem. We have seen how linked lists work in a sequential manner. We saw linked lists working in a sequential manner and observed how programming applications use stacks and queues, but these data structures are very restricted. The biggest problem while dealing with linear data structure is that if we have to conduct a search, the time taken increases linearly with the size of data. Wheareas there are some cases where linear structures can be really helpful but the fact remains that they may not be a good choice for situations that require high speed. Let’s start How to implement Tree Data Structure Using Python.

So, now let’s move on from the concept of linear data structures to nonlinear data structures called trees. Every tree has a distinguished node called the root. Unlike real-life trees, the tree data structure branches downward from parent to child, with every node except the root connected by a direct edge from exactly one other node.

A is the root and it is parent to three nodes — B,C and D.

Same way B is parent to E and C is parent to F and G.

Nodes like D, E, F and G that have no children are called leaves or external nodes. Nodes that have at least child such as a B and C are internal nodes. The number of edges from root to node is called the depth or level of a node. Depth of B is 1 whereas depth of G is 2. Height of a node is the number of edges from the node to the deepest leaf.

B, C, and D and siblings they ahve same parents A. Similarly, F and G are also siblings because they have same parent C.

Children of one node are independent of children of another node.

Every leaf node is unique

The file system that we use on our computer machines is an example of tree structure.
We know additional informations about the node as payload. Although algorithms do not gives much importance to payload, it play a very important role in modern-day computer applications.
An edge connects two nodes to show that there is a relationship between them.
There is only one incoming edge to every node(Except the root). However, a node may have several outgoing edges.
Root of the tree is the only node of the tree that has no incoming edges as it marks the starting point for a tree.
Set of nodes having incoming edges from the same node are the children of that node.
A node is a parent of all the nodes that connect to it by the outgoing edges.
We call a set of nodes and edges that comprises a parent along with all its descendant subtrees.
A unique path traverses from the root to each node.
We call a tree with a maximum of two children a binary tree.

Recursive definition of a tree

A tree can be empty, or it may have a root with zero or more subtree.

An edge connects the roots of every subtree to the root of a parent tree.

Simple Tree Representation

Have a look at following tree. Here, we are considering case of binary tree.

In case of a binary tree, a node cannot have more than two children. So, for ease of understanding, we can say that preceding scenario is similar to something like this:

In this diagram, left and right are references to the instances of node that are located on the left and right of this node respectively. As you can see, every node has three values:

Data
Reference to child on left
Reference to child on right

So, the constructor for the node class to create a Node object will be as follows:

Now let’s create the Node class

So, this is how a root node is created:

When we excute this block of code, the output is as follow:

Create Root Node

Now, we write code for inserting values to the left or right.

When creating a nodes, its left and right references initially point to None.

And a child can be added to right in the similar way:

However, if the root nodes already points to an existing child and we attempt to insert a child nodes, we should push the existing child down one level, and the new object should take its place. Therefore, we pass on the reference of the existing child stored in self.left to child.left, and then we assign self.left the reference to child. You can achieve this in the following manner.

What is the definition of a tree?

A tree is a set of nodes that store elements. The nodes have parent-child relationship such that:

If the tree is not empty, it has a special node called the root of tree. The root has no parents.
Every node of the tree different from the root has a unique parent node.

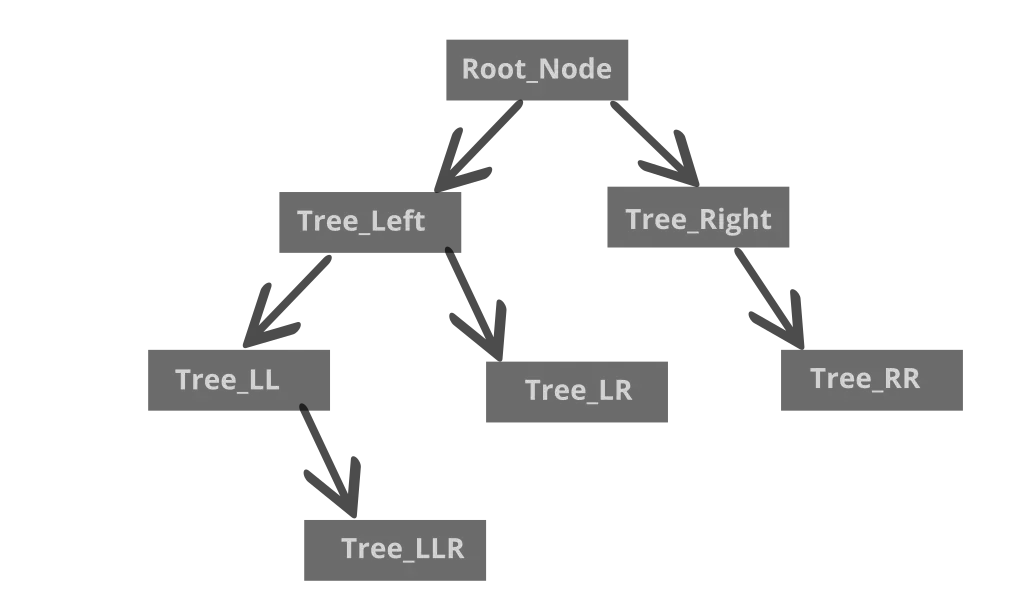
Representing a tree as list of lists

In list of lists, we shall store the value of the node as the first element. The second elementwill be the list that represents the left subtree and the third element represents the right subtree. The following figure shows a tree with just the root node.

Now, suppose we add a node to the left.

Now, adding another subtree to the right would be equal to:

Same way adding a node to the left of Tree_Left can be done as shown in figure

Here you can see that the tree can be defined as follows:

Here, the root is Root_Node which is located at binary_tree[0].

Left subtree is at binary_tree[2]

How to implement Tree Data Structure Using Python

Now let’s write the code for this:

Step 1: Define class

class Tree:

Step 2: Create constructor

Now let’s write the code for constructor. Here, when we create an object we pass a value. The constructors creates a list with the value placed at index 0, and with empty lists at indices 1 and 2. If we have to add subtree at the left side we will do so at index 1 and for right subtree we will insert values in the list at index 2.

	def __init__(self, data):
		self.tree = [data, [], []]

Step 3: Define function to insert left and right subtree

If you have to insert a value in left sub tree then pop the element at index 1 and insert the new list at that place. Similarly, if you have to insert a child at right hand side, pop the value at index 2 and insert the new list.

		def left_subtree(self, branch):
			left_list = self.tree.pop(1)
			left.tree.insert(1, branch.tree)


		def right_subtree(self, branch):
			right_list = self.tree.pop(2)
			self.tree.insert(2, branch.tree)

Now let’s execute the code:

Code

class Tree:
	def __init__(self, data):
		self.tree = [data, [], []]


		def left_subtree(self, branch):
			left_list = self.tree.pop(1)
			left.tree.insert(1, branch.tree)


		def right_subtree(self, branch):
			right_list = self.tree.pop(2)
			self.tree.insert(2, branch.tree)

Output

There is however one thing ignored in this code. What if we want to insert a child somewhere in between? Here, in this case the child will be inserted at the given location and the subtree existing at that place will be pushed down.

For this we make changes in the insert functions.

def left_subtree(self, branch):
	left_list = self.tree.pop(1)
	if len(left_list) > 1:
		branch.tree[1] = left_list
		self.tree.insert(1,branch.tree)
	else:
		self.tree.insert(1,branch.tree)

If we have to insert a child in the left then first we pop the element at index 1. If the length of element at index 1 is 0 then, we simply insert the list. However, if the length is not zero then we push the element to the left of the new child. The same happens in case of right subtree.

	def right_subtree(self, branch):
		right_list = self.tree.pop(2)
		if len(right_list) > 1:
			branch.tree[2]=right_list
			self.tree.insert(2,branch.tree)
		else:
			self.tree.insert(2,branch.tree)
print("Create TreeLL")
treell = Tree("TreeLL")
tree_left.left_subtree(treell)
print("Value of TREE = ",root.tree)

Code

class Tree:
	def __init__(self,data):
		self.tree = [data, [], []]

	def left_subtree(self, branch):
		left_list = self.tree.pop(1)
		if len(left_list) > 1:
			branch.tree[1] = left_list
			self.tree.insert(1,branch.tree)
		else:
			self.tree.insert(1,branch.tree)

	def right_subtree(self, branch):
		right_list = self.tree.pop(2)
		if len(right_list) > 1:
			branch.tree[2]=right_list
			self.tree.insert(2,branch.tree)
		else:
			self.tree.insert(2,branch.tree)

Execution

print("Create Root Node")
root = Tree("Root_node")
print("Value of Root = ",root.tree)
print("Create Left Tree")
tree_left = Tree("Tree_Left")
root.left_subtree(tree_left)
print("Value of Tree_Left = ",root.tree)
print("Create Right Tree")
tree_right = Tree("Tree_Right")
root.right_subtree(tree_right)
print("Value of Tree_Right = ", root.tree)
print("Create Left Inbetween")
tree_inbtw = Tree("Tree left in between")
root.left_subtree(tree_inbtw)
print("Value of Tree_Left = ",root.tree)
print("Create TreeLL")
treell = Tree("TreeLL")
tree_left.left_subtree(treell)
print("Value of TREE = ",root.tree)

Output

Create Root Node
Value of Root =  ['Root_node', [], []]
Create Left Tree
Value of Tree_Left =  ['Root_node', ['Tree_Left', [], []], []]
Create Right Tree
Value of Tree_Right =  ['Root_node', ['Tree_Left', [], []], ['Tree_Right', [], []]]
Create Left Inbetween
Value of Tree_Left =  ['Root_node', ['Tree left in between', ['Tree_Left', [], []], []], ['Tree_Right', [], []]]
Create TreeLL
Value of TREE =  ['Root_node', ['Tree left in between', ['Tree_Left', ['TreeLL', [], []], []], []], ['Tree_Right', [], []]]